In recent explorations, I've delved into introductory microeconomics, game theory, and related subjects. Among the plethora of fascinating concepts, I was particularly intrigued by foundational theories such as the Nash equilibrium. This piqued my curiosity and led me to contemplate and consolidate my thoughts, prompting the creation of this article.
Game theory, a mathematical study of strategic decision-making, delves into the concept of Nash equilibrium. Nash equilibrium represents a scenario in which no player can unilaterally improve their position by changing their strategy. However, this equilibrium does not always align with the socially optimal outcome, which maximizes collective welfare.

The Nash equilibrium is a central idea in game theory because it represents a point where players’ expectations are met, and no one has anything to gain by changing their strategy alone. It is named after John Nash, who demonstrated that every finite game has at least one Nash equilibrium, possibly in mixed strategies.

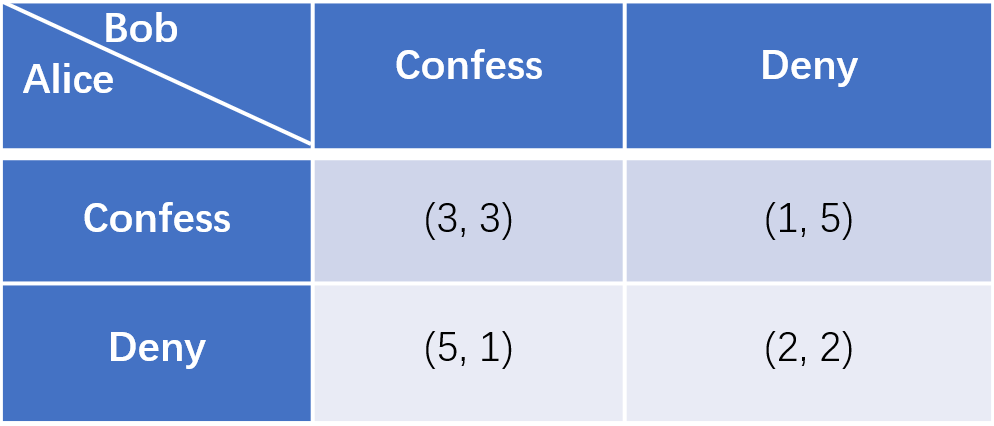
In the scenario depicted, if both players choose to “Confess,” they each receive a payoff of 3. This outcome, while not the most beneficial for either player, represents a Nash Equilibrium. It’s a stable state where neither Alice nor Bob can improve their situation by changing their strategy unilaterally, assuming the other’s strategy remains unchanged. This equilibrium is not the optimal collective outcome, which would be achieved if both players chose to “Deny,” resulting in a payoff of 2 for each. However, the fear of receiving the lowest payoff (1) if the other player betrays them (by confessing while they deny) drives both players to choose “Confess,” leading to a mutually worse outcome of 3 each.
The Nash Equilibrium here illustrates a significant problem: rational individuals might not cooperate, even when it seems that cooperation would be in their best interest. This paradox is evident in various real-world situations where individual incentives lead to collective suboptimal outcomes, such as in competitive business environments, political negotiations, or public goods dilemmas. The Prisoner’s Dilemma thus serves as a powerful tool for understanding strategic interactions in economics, politics, and sociology, highlighting the complexity of human decision-making processes.
The Nash equilibrium has profound implications beyond theoretical models. It has been applied to various fields, including economics, politics, and biology. For instance, it helps explain market behaviors in oligopolies, voting strategies in elections, and even the behavior of species in an ecosystem.
However, it’s important to note that Nash equilibrium does not necessarily result in the optimal outcome for all players involved. It simply means that given the current strategies, no one player can do better by changing their strategy alone. This can lead to situations where all players are worse off than if they could somehow coordinate and agree on a different set of strategies—a concept known as Pareto inefficiency.
In real-world scenarios, achieving Nash equilibrium can be complex due to the multitude of factors influencing decision-making. Communication, trust, and the potential for future interactions can all play a role in whether players adhere to the equilibrium or seek to deviate in pursuit of better outcomes.

Unlike the notion posited by Adam Smith in The Wealth of Nations or An Inquiry into the Nature and Causes of the Wealth of Nations that individuals pursuing self-interest will lead to the best societal outcomes, Nash's theory suggests that people in real life do not always act in a way that leads to the greatest collective benefit. Even though individuals may share a common goal, they may be pulling in different directions. Therefore, the summation of individual interests does not necessarily equate to the overall welfare of society. In the realm of game theory, it is crucial to consider the decisions of each participant, as optimizing personal decisions does not always guarantee the best overall outcome.
Just like the classic "prisoner's dilemma," game theory presents an abstract and simplified model of real-life scenarios. While models can shed light on certain real-world issues, the complexity of real-life situations far surpasses that of theoretical models. The prisoner's dilemma exemplifies the conflict between individual rationality and collective benefit, where cooperation may be collectively rational but individually irrational.
In essence, the Nash equilibrium exemplified in the prisoner's dilemma showcases the paradox where individual rationality leads to a suboptimal outcome for all parties involved. This highlights the challenge of reconciling self-interest with the well-being of society as a whole. However, game theory provides strategies such as repeated interaction, communication, and reputation-building to navigate these challenges and encourage cooperation.
Nevertheless, game theory offers mechanisms like repeated interactions, communication, and reputation management to mitigate these challenges and foster cooperation. Understanding the interplay between Nash equilibrium and social welfare enriches our comprehension of strategic decision-making. It prompts us to seek a balance between individual actions and communal benefits amidst the dense network of strategic dependencies. Through this perspective, we gain a deeper understanding of the subtleties inherent in strategic choices and their impact on both individual and collective prosperity